아르키메데스 전기, 기고 및 발명품
시러큐스의 아르키메데스 (287 a.C - 212 a.C)는 시칠리아 섬의 고대 시라쿠사 (Syracuse)시에서 수학자, 물리학 자, 발명가, 엔지니어 및 그리스 천문학 자였습니다. 그의 가장 탁월한 공헌은 아르키메데스 (Archimedes)의 원리, 외래 방식의 개발, 기계적 방법 또는 최초의 플라네타륨 창조.
자신의 기여는 수학, 물리학, 기하학과 천문학의 분야에서 시간에 중요한 과학적 진보를 의미 그것은 현재, 유클리드와 아폴로와 고대의 수학에서 가장 중요한 세 인물의 하나로서 간주됩니다. 차례로, 이것은 인류의 역사에서 그에게 최고의 과학자 중 하나를 만든다.

그의 개인의 몇 가지 세부 사항 생활-및 알려진 사람들은 속하는 오늘날까지 보존되어 자신의 작업과 성과에 대한 쓴 편지의 일련의 의문 신뢰성 알려진, 그들의 공헌이 알려진 덕분에,하지만 그가 시간의 친구 및 다른 수학자와 수년간 지낸 통신에.
아르키메데스 (Archimedes)는 그의 동시대 인들의 관심을 끌었던 발명품 덕분에 시간이 유명했는데 부분적으로 로마의 침략을 피하기 위해 전쟁 장비로 사용 되었기 때문입니다..
그러나 그는 정말로 중요한 것은 수학이라고 주장했으며 그의 발명품은 응용 기하학의 과거의 산물이라고 주장했다. 후손의 순수 수학에 대한 그의 작품은 그의 발명품보다 훨씬 더 감사하게 여겨져왔다..
색인
- 1 전기
- 1.1 교육
- 1.2 과학적 연구
- 1.3 시러큐스의 갈등
- 1.4 죽음
- 2 아르키메데스의 과학적 기여
- 2.1 아르키메데스의 원리
- 2.2 기계적인 방법
- 2.3 레버의 법칙에 대한 설명
- 2.4 과학 시연을위한 첨단 또는 고갈 방법 개발
- 2.5 원의 척도
- 2.6 구 및 원기둥의 기하학
- 발명 3 점
- 3.1 주행 거리계
- 3.2 첫 번째 플라네타륨
- 3.3 아르 키 메데스 나사
- 3.4 아르키메데스의 발톱
- 4 참고
약력
Syracuse의 아르키메데스는 대략 BC 287 년에 태어났습니다. 시칠리아 섬의 주요 항구로 간주되는 도시인 시러큐스에서 태어났다는 것은 말할 필요도 없지만 그의 초기시기에 대해서는별로 알려지지 않았다..
그 당시, 시라쿠사는 소위 말하는 마그나 그리스 (Magna Grecia)라는 도시 중 하나였습니다.이 도시는 그리스 원산지의 이주민들이 이탈리아 반도와 시칠리아 남부 지역에 거주하는 공간이었습니다.
아르키메데스의 어머니에 대한 알려진 사실은 없습니다. 아버지와 관련해서는 이것이 피디 아스 (Phidias)라고 불렸고 천문학에 전념했다고 알려졌습니다. 그의 아버지에 대한이 정보는 책의 일부분으로 알려져있다. 모래 카운터, 아르키메데스 (Archimedes) 지음 : 아버지의 이름을 언급 함.
그리스 철학자이자 천문학자인 헤라클레스는 아르키메데스를 아주 좋아했으며 그에 관한 전기도 썼다. 그러나이 문서는 보존되지 않았으므로 여기에 포함 된 모든 정보를 알 수 없습니다..
또한, 역사 학자, 철학자이자 전기 작가 플루타르코스는 그의 책 병렬에 명시된 아르키메데스가 Hiero II, 265 BC부터 시러큐스에서 명령 폭군 혈액에 의해 관련이 있음을 사는.
교육
우리가 아르키메데스에 관해 가지고있는 작은 정보의 결과로, 우리는 그가 어디에서 첫 번째 훈련을 받았는지 알지 못합니다.
그러나 다양한 역사 학자들은이 지역의 가장 중요한 그리스 문화 및 교육 센터였던 알렉산드리아에서 아르 키메데스가 공부할 가능성이 높다고 결론지었습니다..
이 가정은 그리스 역사가 인 Diodoro Sículo가 제공 한 정보에 의해 뒷받침된다. Archimedes는 아마도 Alexandria.
또한 그의 작품 대부분에서 아르키메데스는 알렉산드리아에 집중되어 있던 당시의 다른 과학자들에 대해 언급하고 있기 때문에 그는 실제로 그 도시에서 발전했다고 추정 할 수 있습니다.
아르키메데스가 알렉산드리아에서 상호 작용 한 것으로 여겨지는 인물들 중 일부는 지리학자, 수학자이자 천문학자인 에레토스테네스 (Cyrene), 수학자이자 천문학 자 Conon de Sanos.
가족 동기 부여
반면에, 아르 키 메데스의 아버지는, 천문학 때문에 나중에 젊은 나이에서 나중에 demostróe 경사에 크게 영향을 미쳤을 수있는 사실이었다 그를의 영역에 특별한 매력 분명했다 과학.
알렉산드리아에서 근무한 후, 아르키메데스는 시러큐스로 돌아갔다..
과학적 연구
시러큐스로 돌아온 후에 아르키메데스는이 도시의 주민들에게 곧 인기를 얻은 다양한 인공물을 고안하기 시작했습니다. 이 기간에 그는 자신을 과학 연구에 완전히 투입하고, 다른 발명품을 만들어 내며, 여러 수학적 개념을 그의 시대까지 발전 시켰습니다.
예를 들어, 그는 단단한 곡면과 평면 인물의 특성에 대한 연구에 몰두했을 때, 나중에 발달 한 적분 및 미분 계산과 관련된 개념을 생각해 냈습니다.
또한 아르키메데스 (Archimedes)는 구체와 관련된 체적이 실린더의 크기의 두 배에 해당하고, 레버의 법칙에 대한 발견을 바탕으로 복합 풀리를 발명 한 사람이라고 정의한 사람입니다.
시러큐스의 충돌
기원전 213 년 동안 로마 군인들은 시러큐스시에 들어서 정착민을 포위하여 포기하게했다..
이 행동은 군대와 그리스 정치가 마르코 클라우디오 마르첼로 (Marco Claudio Marcelo)가 2 차 포니 전쟁 (Punic War)의 틀 안에서 주도했다. 나중에 그것은 Syracuse를 정복 한 이후 로마의 검으로 알려져있었습니다..
이 도구와 장비 개발에 주력하고 이후 이년 지속 된 갈등의 한 가운데에서, 로마를 격파하는 데 도움이, 로마에 대한 시러큐스의 주민들은 용기와 사나움과 싸웠다, 그리고 아르키메데스는 매우 중요한 역할을.
마지막으로 Marco Claudio Marcelo는 시러큐스시를 택했습니다. 아르키메데스의 위대한 지적이 있기 전에 마르셀로는 상처를 입히거나 살해하지 말 것을 명령했습니다. 그러나 아르키메데스는 로마 병사의 손에 죽었다..
죽음
아르키메데스는 기원전 212 년에 사망했다. 그가 사망 한 지 130 년이 지난 137 년, 작가이자 정치가이자 철학자 인 마르코 툴 리오 키 세로 (Marco Tulio Cicero)는 로마 행정부에서 지위를 차지하고 아르키메데스의 무덤을 찾고 싶었다..
이 작업은 Cicero가 정확한 장소를 나타내는 사람을 찾을 수 없었기 때문에 쉽지 않았습니다. 그러나, 그는 결국 아그 리젠 토의 문과 매우 가까운 조건에서 그것을 얻었다..
키케로는이 무덤을 청소하여 아키 스톡이 얼마 전에 만든 부피에 대한 발견에 대한 참고 자료로 실린더 안의 구형이 새겨 져 있음을 발견했습니다..
그의 죽음에 관한 버전들
첫 번째 버전
버전 중 하나는 아르키메데스가 로마 병사가 접근했을 때 수학 문제를 푸는 중반에 있다고 말합니다. 아르키메데스가 그 문제를 해결할 시간을 물어볼 수도 있었으므로 병사가 그를 죽였을 것이다..
두 번째 버전
두 번째 버전은 첫 번째 버전과 유사합니다. 아르키메데스가 도시를 점령했을 때 수학 문제를 해결했다는 기사.
로마 병사가 자신의 화합물을 들어서 마르셀로를 만날 것을 명령했고 아르키메데스는 자신이 먼저 해왔 던 문제를 해결해야한다고 대답했다. 군인은이 응답의 결과로 화가 나서 그를 죽였다..
세 번째 버전
이 가설은 아르키메데스가 수학에 전형적으로 중요한 악기를 다양하게 보유하고 있음을 나타냅니다. 그런 다음 병사가 그를보고 귀중한 물건을 소지하고 있다고 생각하여 그를 죽였다..
네 번째 버전
이 버전은 아르키메데스는 그가 공부 비행기를보고, 땅 근처에 웅크 리고있는 것을 보여줍니다. 분명히, 로마 군인은 아르키메데스 샷 것을 알지 못하고, 뒤에서 와서.
아르키메데스의 과학적 기여
아르키메데스의 원리
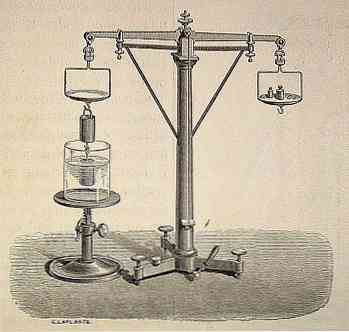
아르키메데스의 원리는 현대 과학이 고대 시대의 가장 중요한 유산 중 하나로 여기는 것으로 간주됩니다.
역사, 구강 maneral 전반에 걸쳐, 그를 위해 만들어 의뢰 골드 크라운은 금이 이루어 졌는지 여부를 아르키메데스 확인 맡기는 것이다 그의 발견에 킹 Hiero에 실수 덕분에 온 전해지고있다 순수하고 다른 금속을 포함하지 않았다. 나는 왕관을 파괴하지 않고이 작업을 수행했다.
아르키메데스가이 문제를 해결하는 방법을 명상하는 동안 그는 목욕하기로 결심했으며, 욕조에 들어갔을 때 그는 물에 잠긴 상태에서 물의 양이 증가했다는 것을 깨달았습니다..
이런 방식으로, 그는 "유체 (액체 또는 가스)에 전체적으로 또는 부분적으로 잠긴 모든 몸체가 물체에 의해 제거 된 유체의 무게와 동일한 상향 추력을 받았다"는 과학적 원리를 발견하게 될 것입니다..
이 원리는 유체가 그 안에 침지 상향 개체 푸시 상향 힘을 발휘하고 있음이 부력의 중량에 관계없이 침지 체로 변위 액체의 중량을 동일하다는 의미.
이 원리에 대한 설명은 부상의 현상을 설명하며, 육체에 관한 조약.
아르키메데스의 원칙은 잠수함, 선박, 생명 원 및 풍선과 같은 거대한 용도의 물체를 떠 다니는 자손에게 크게 적용되었습니다.
기계적 방법
과학 아르키메데스에 가장 중요한 공헌의 또 다른 시간에 대한 이러한 문제를 해결하기 위해 전례없는 방법을 의미 기하학적 문제의 말씀 - 그건 순전히 기계적인 방법을 포함, 기술 추론과 논증을했다.
아르키메데스의 맥락에서, 기하학은 독점적으로 이론 과학으로 간주되었으며, 공통된 것은 순수 수학이 그 원리가 적용될 수있는 다른 실용 과학으로 내려 갔다는 것이 었습니다..
이런 이유로, 오늘날 그것은 과학 분야로서의 역학의 선구자로 간주됩니다.
수학은 그의 친구 에라 토 스테 네스에 새로운 방법을 노출하는 편지에서, 그것은 역학을 통해 수학의 문제를 해결할 수 있음을 나타냅니다, 어떤 방법으로 경우 이미 기하학 정리의 데모를 구축하는 것이 더 쉽습니다 이전에 실용적인 지식을 가지고 있다면, 그것에 대해 전혀 모른다면.
아르키메데스가 수행 한이 새로운 조사 방법은 현대 과학 방법의 발견 및 가설 공식화의 비공식적 인 단계의 선구자가 될 것이다.
레버의 법칙에 대한 설명
레버 훨씬 이전 시대 아르키메데스에서 사용하는 간단한 기계이지만, 그는이 비행기의 균형에 자신의 논문에서 작동하는 방법에 대해 설명 원리를 공식화 사람이었다.
이 법칙을 수립 할 때 아르키메데스 (Archimedes)는 무게와 지지점으로부터의 거리에 따라 두 개의 시체를 놓을 때의 레버의 다른 동작을 설명하는 원리를 수립합니다.
이런 식으로 그는 레버에 위치한 측정 가능한 (보상 가능) 두 몸체가 몸무게에 반비례하는 거리에있을 때 균형을 이룬다 고 지적합니다.
마찬가지로, (측정 할 수없는)를 잴 수없는 몸을하지만,이 법은 아르키메데스에 의해 첫 번째 유형의 몸 입증했다.
레버의 원리에 대한 공식은 기계적 방법의 적용에 대한 좋은 예입니다. Dositeo에게 보낸 서한에서 설명했듯이, 실제로이 기계는 처음에 실제로 적용된 기계의 방법을 통해 발견되었습니다.
나중에 그들은 기하학의 방법 (이론적)을 사용하여 그들을 공식화했다. 이 시체에 대한 실험에서도 중심의 개념이 분리되었다..
과학 시연을위한 배출 또는 배출 방법 개발
고갈은 형상이 알려진 기하학적 인 도형과 비문 및 외접에 의해 알려진 기하학적 인 도형으로 구성된 기하학에서 사용되는 방법입니다..
아르키메데스는이 방법의 창시자가 아니었지만 그것을 훌륭하게 개발하여 Pi의 정확한 값을 계산했다..
아르키메데스, exhaution의 방법을 사용하여, 직경 1의 원주에 새겨 넣고 외접 육각형, 육각형의 영역과 원주의 영역 사이의 차이를 터무니없이 감소.
이를 위해 그는 앞의 그림에서와 같이 육각형을 2 등분하여 최대 16면의 다각형을 만듭니다..
이 방법으로, 그는 원의 길이와 직경 사이의 관계의 pi 값이 3.14084507 ...과 3.14285714 사이에 있음을 지정하게되었습니다. .
단지 매우 낮은 오차는 원주율의 값을 계산하는 방법을 관리하므로 deseado- 아니라 통해 무리수 파이 되 때문에 아르키메데스 훌륭하게 고갈의 방법을 사용한 이 방법과 결과는 현대 적분에, 이후에 시스템 미적분학에서 발아 할 수있는 토대를 마련하고, 얻어진.
원의 크기
원의 면적을 결정하기 위해 아르키메데스는 원 안에 정확히 들어있는 사각형을 그리는 방법을 사용했습니다.
사각형의 면적이 그 변의 합이고 원의 면적이 더 크다는 것을 알고, 그는 근사치를 구하기 위해 작업하기 시작했습니다. 이것은 정사각형을 6면 다각형으로 바꾸고 더 복잡한 다각형으로 작업함으로써 수행했습니다..
아르키메데스 (Archimedes)는 역사상 최초의 수학자로 파이 (Pi)에 대한 진지한 계산에 접근했다..
구 및 실린더의 기하학
아르키메데스 수학과 물리학 작업을 집계 한 9 개의 논문 중에서 구체와 실린더의 기하학에 관한 두 권의 책이 있습니다.
이 연구는 어떤 구체의 표면이 가장 큰 원형의 표면의 4 배이며, 구체의 체적이 그 표면에 새겨진 실린더의 체적의 3 분의 2라는 결론을 다룬다.
발명품
주행 거리계
일컬어 킬로미터, 그것은이 유명한 남자의 발명품이었다..
이 장치는 회전 할 때 이동 거리를 계산할 수있는 기어를 활성화하는 휠의 원리를 기반으로 제작되었습니다..
이 같은 원칙에 따라 아르키메데스는 군사 및 민간 목적의 여러 가지 유형의 주행 계를 설계했습니다.
첫 번째 플라네타륨
키케로, 오비디우스, 클라우디우스, 마르시 아노 Capela의, Casiodoro, 섹스 투스 엠피 리 쿠스와 Lactancio, 오늘 같은 많은 고전 작가의 증언을 바탕으로 많은 과학자 아르키메데스에 처음 초보 행성의 생성 특성.
이것은 행성들의 움직임을 모방 할 수있는 일련의 "구체들"로 구성된 메커니즘입니다. 지금까지이 메커니즘의 세부 사항은 알려져 있지 않습니다..
키케로 (Cicero)에 따르면 아르키메데스 (Archimedes)가 만든 플라네타륨은 2 종류였습니다. 그들 중 하나에서 그 땅과 그 주변의 다양한 별자리가 나타났습니다..
다른 한편으로, 한 번의 회전으로 해와 달과 행성은 실제 별에서와 같은 방식으로 고정 된 별과 관련하여 그들 자신의 독립적 인 움직임을 만들었다. 후자에서, 또한, 달의 연속 위상과 일식을 관찰 할 수 있었다.
아르키메데스의 나사
아르키메데스 스크류는 튜브 또는 실린더를 사용하여 물을 경사면을 통해 아래에서 위로 운반하는 데 사용되는 장치입니다.
그리스 역사 학자 디오도로 (Diodoro)에 따르면,이 도구 덕택에 고대 이집트의 나일강 강가에 위치한 비옥 한 토지의 관개가 용이 해졌습니다. 전통적인 도구는 노동자들에게 지친 막대한 물리적 노력이 필요했기 때문입니다.
사용 된 실린더는 회전 레버에 의해 수동으로 구동되는 회전 운동을 수행하는 프로펠러 또는 핀 시스템과 상호 연결된 상태를 유지하는 동일한 길이의 나사 내부에 있습니다.
이 방법으로, 나선은 물질을 바닥에서 위로 밀면서 일종의 무한 회로를 형성합니다..
아르키메데스의 발톱
아르키메데스의 발톱 또는 철의 손은이 수학자가 만든 전쟁 중 가장 무서운 무기 중 하나였으며 로마 침략에 대한 시실리 방어의 가장 중요한 요소가되었습니다.
드렉 셀 크리스 Rorres (수학과)와 해리 해리스 (토목 공학 및 건축학)의 대학에서 교수가 실시한 연구에 따르면, 레버에 부착 된 갈고리를 가지고 큰 레버를했습니다 그녀의 주위에 체인에 의해.
그래서 레버를 통해 후크 적 선박에 떨어졌다 조작되었고, 목표는 후크와 방출이 뒤집거나 해안의 바위에 충돌하게 완전히 달성되었다 정도로으로 인상했다.
Rorres와 해리스는 심포지엄 "기계 및 고대의 특별한 구조"(2001), 자격이 기기의 소형 표현에서 발표 된 "강력한 전쟁 기계 : 아르키메데스의 철 손의 건설 및 운영"
이 작품의 실현을 위해 그들은 고대 역사 학자 인 폴리 비오 (Polibio), 플루타르코 (Plutarco), 티토 리비 오 (Tito Livio)의 주장에 의존했다..
참고 문헌
- ASSIS, A. (2008). 아르 키 메데스 (Archimedes), 중력의 중심, 그리고 역학의 첫 번째 법칙 [온라인]. 2017 년 6 월 10 일 bourabai.ru에서 접속.
- DIJKSTERHUIS, E. (1956). 아르 키 메데스 [온라인]. 2015 년 6 월 9 일 월드 와이드 웹에서 액세스 : books.google.co.ve/books.
- 몰리나, 에이. (2008). 시러큐스의 아르키메데스 (Archimedes of Syracuse) 연구 방법 : 직관, 역학, 실사 [온라인]. 2017 년 6 월 10 일 World Wide Webproduccioncientifica.luz.edu에서 액세스.
- O'CONNOR, J. & ROBERTSON, R. (1999). Syracuse의 Archimedes [온라인]. 2017 년 6 월 9 일 history.mcs.st-and.ac.uk에서 액세스.
- PARRA, E. (2009). 아르 키 메데스 (Archimedes) : 그의 삶, 작품 및 현대 수학에 대한 공헌 [온라인]. 2017 년 6 월 9 일 lfunes.uniandes.edu.co에서 검색 함.
- QUINN, L. (2005). Syracuse의 Archimedes [온라인]. 2017 년 6 월 9 일, math.ucdenver.edu에서 액세스.
- RORRES, C. & Harris, H. (2001). 조밀 한 전쟁 기계 : Archimedes의 Iron Hand [온라인]의 건설 및 운영. 2017 년 6 월 10 일 cs.drexel.edu에서 검색 함.
- VITE, L. (2014). 아르키메데스의 원리 [온라인]. 2017 년 6 월 10 일 repository.uaeh.edu.mx에서 검색 함.


