동일 시스템 및 예제
그 공선 벡터 그것들은 기존 벡터의 세 가지 유형 중 하나입니다. 그것은 같은 방향이나 행동 행로에있는 벡터에 관한 것입니다. 즉, 두 개 이상의 벡터가 서로 평행 한 직선으로 배열되어 있으면 두 개 이상의 벡터가 동일 선상에 있습니다..
벡터는 몸에 적용되는 양으로 정의되며 방향, 감각 및 척도를 갖는 것으로 특징 지어집니다. 벡터는 평면 또는 공간에서 찾을 수 있으며 여러 유형이있을 수 있습니다 : 공선 벡터, 동시 벡터 및 평행 벡터.

색인
- 1 colineal 벡터
- 2 특성
- 2.1 예제 1
- 2.2 예제 2
- 2.3 예제 1
- 3 공선 벡터 시스템
- 3.1 반대 감각을 가진 공선 벡터
- 3.2 같은 감각을 가진 동일 선상의 벡터들
- 3.3 같은 크기와 반대 감각을 가진 동일 선상의 벡터들
- 4 공선 벡터와 동시 벡터의 차이점
- 5 참고
공선 벡터
벡터의 크기와 감각에 관계없이, 하나의 행동 행이 다른 모든 벡터의 행동 행렬과 정확히 일치하면 벡터는 동일 선상에 있습니다..
벡터는 수학, 물리학, 대수학 및 기하학과 같은 여러 분야에서 표현으로 사용되며, 벡터의 방향이 동일 할 때만 벡터가 공존합니다..
특징
- 두 개 이상의 벡터는 좌표 간의 관계가 동일하면 동일 선상에 있습니다..
예제 1
우리는 벡터 m = m_x; m_y 및 n = n_x; n_y. 다음 경우에 동일 선상에 있습니다.
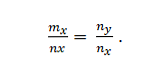
예제 2
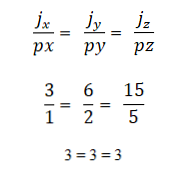
- 곱 또는 벡터 곱셈이 0 인 경우 두 개 이상의 벡터가 동일 직선 상입니다. 이것은 좌표계에서 각 벡터가 해당 좌표로 특성화되고 서로 비례하면 벡터가 동일 선상에 있기 때문입니다. 이것은 다음과 같이 표현됩니다.
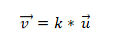
예제 1
벡터는 a = (10, 5)와 b = (6, 3)입니다. 이들이 동일 선상에 있는지 결정하기 위해 결정 성 이론이 적용되어 교차 산물의 평등성을 확립합니다. 그런 식으로, 당신은해야한다 :
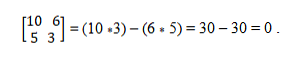
공선 벡터 시스템
동일 선상의 벡터는 방향과 의미를 사용하여 그래픽으로 표현되며, 응용 프로그램의 지점과 모듈을 통과해야한다는 것을 고려합니다 (특정 축척 또는 길이).
동일 선상의 벡터 시스템은 두 개 이상의 벡터가 물체 또는 몸체에 작용할 때 형성되며 힘을 나타내고 같은 방향으로 작용합니다.
예를 들어 몸에 두 개의 동일 선상의 힘이 적용되면 이들의 결과는 동작하는 방향에만 의존합니다. 다음 세 가지 경우가 있습니다.
반대 감각을 가진 공선 벡터
두 개의 동일 선상의 벡터의 합은 다음의 합과 같습니다.
R = Σ F = F1 + F2.
예제
카트에 2 개의 힘이 작용하면 F1 = 40 N 및 F2 = 20 N 반대 방향으로 (이미지에 표시된대로) 결과는 다음과 같습니다.
R = ΣF = (- 40N) + 20N.
R = - 20 N.
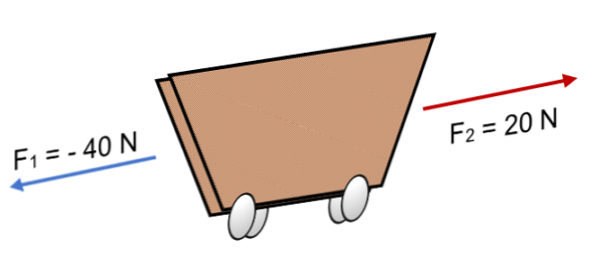
같은 감각을 가진 동일 선상의 벡터들
합력의 크기는 동일 직선 벡터의 합과 같습니다.
R = Σ F = F1 + F2.
예제
카트에 2 개의 힘이 작용하면 F1 = 35 N 및 F2 = 55 N (이미지에 표시된 것과 같은 방향)이면 결과는 다음과 같습니다.
R = ΣF = 35N + 55N.
R = 90 N.
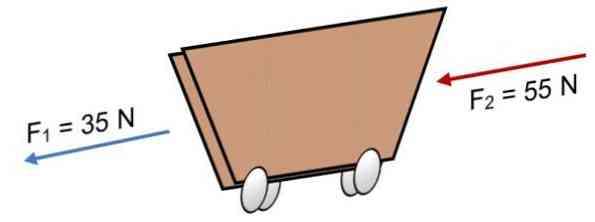
양수 결과는 동일 선상의 벡터가 왼쪽으로 향하는 것을 나타냅니다..
동등한 크기와 반대 감각을 가진 동일 선상의 벡터들
두 개의 동일 선상의 벡터의 결과는 동일 선상의 벡터의 합과 같습니다.
R = Σ F = F1 + F2.
힘은 크기가 같지만 반대 방향, 즉 하나는 양성이고 다른 하나는 음의 힘을가집니다. 두 힘을 더하면 결과는 0이됩니다..
예제
카트에 2 개의 힘이 작용하면 F1 = -7 N 및 F2 = 7 N, 같은 크기지만 반대 방향으로 (이미지에 표시된 바와 같이) 결과는 다음과 같습니다.
R = ΣF = (-7N) + 7N.
R = 0.
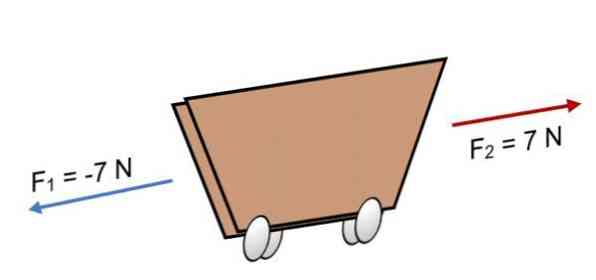
결과는 0이므로 벡터가 서로 균형을 이루므로 신체가 평형에 있거나 휴식 상태에 있음을 의미합니다 (움직이지 않습니다).
동일 선상 벡터와 동시 벡터의 차이점
동일 직선 상에 동일한 방향을 가짐으로써 또는 직선과 평행하기 때문에 동일 직선 벡터는 특징이 있습니다. 즉, 직선 평행선 벡터입니다..
다른 한편, 동시 벡터는 단일 지점에서 가로 챌 수있는 다른 작업 라인에 있기 때문에 정의됩니다.
즉, 모듈, 방향 또는 방향에 관계없이 동일한 원점 또는 도착점을 가지며 두 요소 사이에 각도를 형성합니다.
동시 벡터의 시스템은 힘의 평행 사변형과 힘의 다각형의 방법 인 수학적 방법 또는 그래프에 의해 해결됩니다. 이들을 통해 결과 벡터의 값이 결정되며, 이는 몸체가 움직이는 방향을 나타냅니다.
기본적으로 동일 직선 벡터와 동시 벡터의 주된 차이점은 직선이 동일한 직선에서 동작하는 반면 직선 벡터와 동시 벡터의 주요 차이점.
즉, 동일 선상의 벡터는 단일 평면 "X"또는 "Y"에서 작용합니다. 동일한 지점에서 시작하여 두 비행기에서의 동시 행동.
동일 직선 벡터는 한 점에 있지 않으며, 서로 평행하기 때문에 동시 점 벡터는 점에 없습니다..
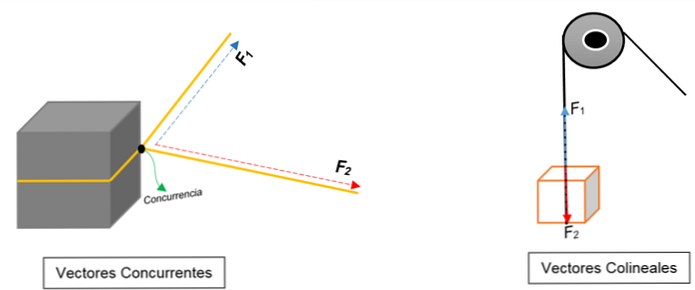
왼쪽 이미지에서 블록을 볼 수 있습니다. 그것은 로프로 묶여 있고 매듭은 두 개로 나눕니다. 상이한 방향 및 다른 힘으로 당겨질 때, 블록은 동일한 방향을 향해 움직일 것이다.
모듈, 감각 또는 방향에 관계없이 한 점 (블록)에서 일치하는 두 벡터가 표현됩니다..
대신 오른쪽 이미지에는 상자를 들어 올리는 풀리가 나타납니다. 로프는 작업 라인을 나타냅니다. 그것이 당겨지면 두 개의 힘 (벡터)이 작용합니다 : 한 번의 힘 (블록을 올릴 때)과 다른 힘 (블록의 무게를 가하는 힘). 둘 다 같은 방향이지만 반대 방향입니다. 어떤 점에서 동의하지 않는다..
참고 문헌
- Estalella, J.J. (1988). 벡터 분석. 제 1 권.
- 굽타, A. (s.f.). 타타 맥그로 힐 교육.
- 진호 흠, S. H. (2015). 선형 대수학. 스프링 어 과학 및 비즈니스 미디어.
- Montiel, H. P. (2000). 기술 학사 학위 물리 1 Patria 편집 그룹.
- Santiago Burbano de Ercilla, C. G. (2003). 일반 물리학 편집 Tebar.
- Sinha, K. (s.f.). 수학 교과서 12 권 2 권. Rastogi Publications.


