서클에는 몇 개의 대칭 축이 있습니까?
그 원의 대칭 축 그들은 무한하다. 이 축은 모든 기하학적 모양을 정확하게 똑같은 두 개의 반으로 나눕니다..
원은 고정 된 점까지의 거리가 특정 값 "r"보다 작거나 같은 모든 점으로 구성됩니다..
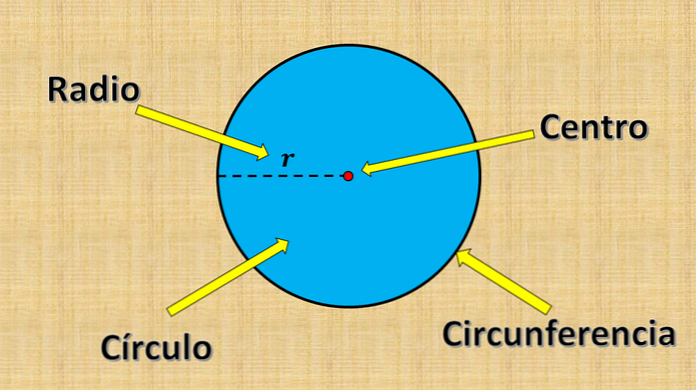
위에서 언급 한 고정 점을 중심이라고하고 값 "r"을 반경이라고합니다. 반경은 원상의 한 점과 중심 사이의 최대 거리입니다.
반면에 끝이 원 (원주)의 가장자리에 있고 중심을 지나는 선분을 직경이라고합니다. 측정은 항상 반경의 두 배입니다..
원과 원주
원과 원을 혼동하지 마십시오. 원주는 중심에서 거리 "r"에있는 점을 나타냅니다. 즉 원의 가장자리 만.
그러나 대칭축을 찾을 때 원 또는 원으로 작업하면 무관합니다..
대칭축이란 무엇인가??
대칭 축은 일정한 기하학적 모양을 두 개의 동일한 부분으로 나누는 선입니다. 즉, 대칭축이 거울처럼 작용합니다..
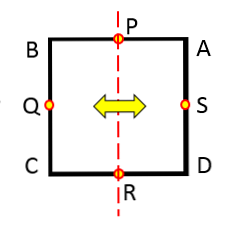
원의 대칭축
반지름에 관계없이 어떤 원이든 관측한다면, 그것을 가로 지르는 모든 선이 대칭축이 아니라는 것을 알 수 있습니다.
예를 들어 다음 이미지에 그려지는 선은 대칭 축이 아닙니다..
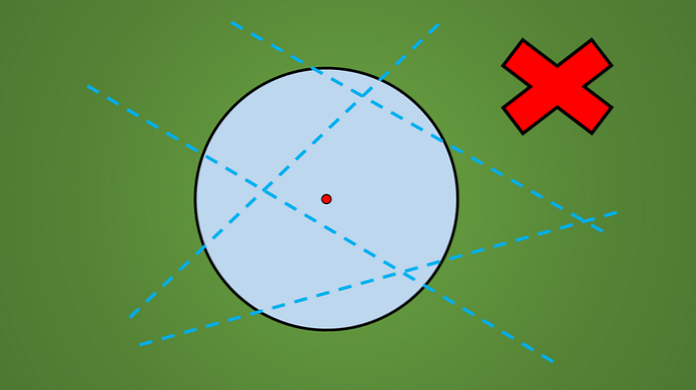
선이 대칭 축인지 아닌지를 쉽게 확인하는 방법은 기하학적 그림을 선 반대편에 수직으로 반영하는 것입니다.
반사가 원래 그림과 맞지 않으면 그 선은 대칭축이 아닙니다. 다음 이미지는이 기법을 보여줍니다..
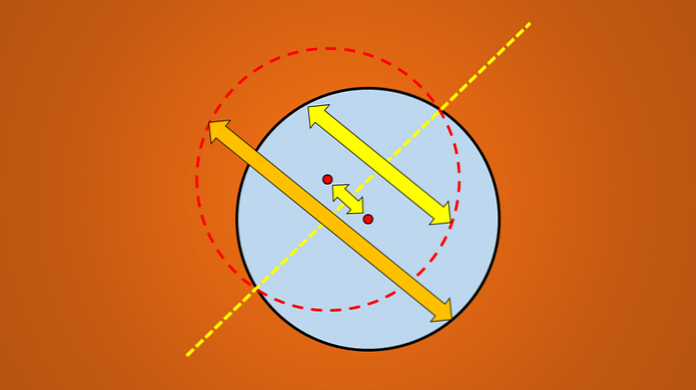
그러나 다음 이미지를 고려할 때 그려진 선은 원의 대칭 축입니다..
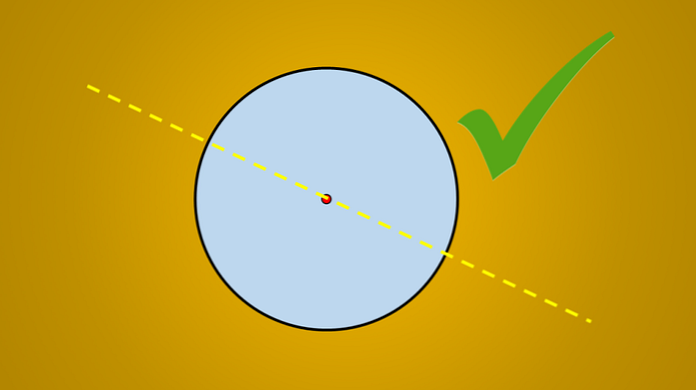
문제는 더 많은 대칭 축이 있습니까? 대답은 '예'입니다. 이 선을 시계 반대 방향으로 45 ° 회전하면 얻은 선이 원의 대칭 축이기도합니다.
90 °, 30 °, 8 ° 및 일반적으로 각도를 임의로 회전하는 경우에도 마찬가지입니다.
이 선들에 대한 중요한 점은 그들이 가진 성향이 아니라 모든 것이 원의 중심을 통과한다는 것입니다. 따라서 원의 지름이 포함 된 선은 대칭 축입니다..
그래서 원은 무한한 수의 직경을 가지므로 무한대의 대칭 축을 갖습니다..
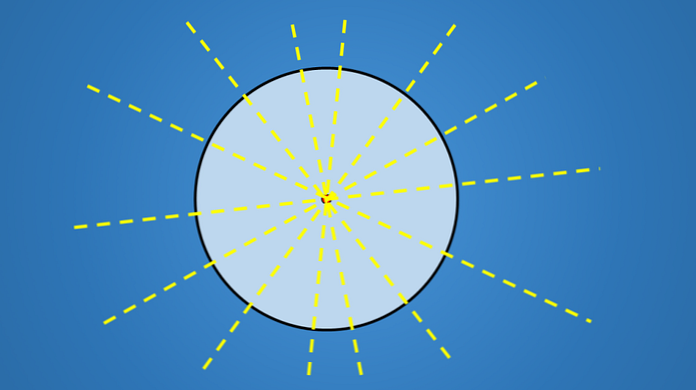
삼각형, 사변형, 오각형, 육각형 또는 다른 다각형과 같은 다른 기하학적 도형은 한정된 수의 대칭 축을 갖습니다.
원이 대칭축의 수를 무한대로 갖는 이유는 변이 없기 때문입니다.
참고 문헌
- Basto, J. R. (2014). 수학 3 : 기본 분석 기하학. Patria 편집 그룹.
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). 수학 : 기초 교육 교사를위한 문제 해결 접근법. 로페스 마테오 편집자.
- Bult, B., & Hobbs, D. (2001). 수학 어휘집 (그림 참조). (카디 나 F. 트라팔가. 에디션) AKAL.
- Callejo, I., Aguilera, M., Martinez, L., & Aldea, C. (1986). 수학 기하학 E.G.B의 상위주기의 개혁. 교육부.
- Schneider, W., & Sappert, D. (1990). 실용 기술 도면 매뉴얼 : 산업 기술 도면의 기본 소개. 되돌리기.
- Thomas, G.B., & Weir, M.D. (2006). 계산 : 여러 변수. 피어슨 교육.


